山西省吕梁市贺昌中学 高永亮 033000
在高中数学中,含变量(一般是字母)问题、构造问题都是难点,学生总感觉比较困难,特别是“构造”问题,更是难度较大。在数列一章中,“构造”问题贯穿了整个章节,构造法是数列的一个重点也是一个难点。笔者在这里进行整理,与广大师生共同探讨。
构造法:是根据数学问题的条件或结论的特征,以问题中的数学为框架、以问题中的数学元素为元件构造出新的数学对象或数字对象或数学模型,从而使问题转化并得到解决;简单地说,构造法:是运用数学的基本思想经过认真的观察,深入的思考,构造出解题的数学模型,从而使问题得以解答.
数列中的构造法:通常有三种.
题型一:由题中的已知式子,再重新构造一个式子,通过两个式子相加减或其它变化解答问题;
题型二:由题中条件直接构造一个或多个式子,再通过这些式子的相互变化解答问题;
题型三:由题中已知式子进行变形,构造新的(模型)式子来解答问题.
一、对教材(新课标)中涉及的内容进行整理:
1.已知数列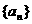 是等差数列,首项为
是等差数列,首项为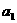 ,公差为
,公差为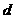 ,求数列
,求数列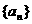 的通项公式.
的通项公式.
解法一:由等差数列的定义,构造:
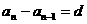
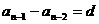

……
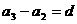

上面各个式子左右两边分别相加,得
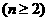 ,
,
当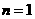 时也符合条件,故
时也符合条件,故 
说明:①一般资料称这种方法为相加相消法.
②本题是题型二.
解法二:教材上的不完全归纳法
由等差数列的定义,得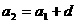 ,
,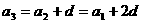 ,
,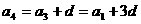 ……猜想:
……猜想:
2. .已知数列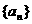 是等比数列,首项为
是等比数列,首项为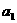 ,公比为
,公比为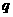 ,求数列
,求数列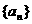 的通项公式.
的通项公式.
解法一:由等比数列的定义,构造:
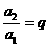
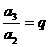
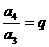
……
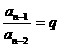

上面各个式子左右两边分别相乘,得
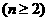 ,
,
当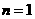 时也符合条件,故
时也符合条件,故
说明:①一般资料称这种方法为相乘相消法.
②本题是题型二.
解法二:教材上的不完全归纳法
由等比数列的定义,得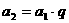 ,
,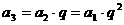 ,
,
……猜想:
3. 已知数列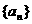 是等差数列,首项为
是等差数列,首项为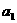 ,公差为
,公差为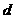 ,求数列
,求数列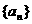 的前
的前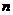 项和
项和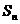 .
.
解:由 ( 1 ) 构造:
( 1 ) 构造:
 ( 2 )
( 2 )
( 1 ) ( 2 )两式左右两边相加得: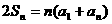
故: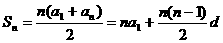
说明:①一般资料称这种方法为倒序相加法。
②.本题是题型二。
4. 已知数列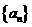 是等比数列,首项为
是等比数列,首项为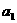 ,公比为
,公比为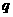 ,求数列
,求数列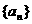 的前
的前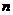 项和
项和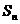 。
。
解:由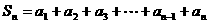 ( 1 )
( 1 )
得 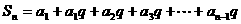 ( 2 )
( 2 )
当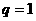 时,
时,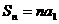
当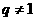 时,由( 1 )式两边分别乘以
时,由( 1 )式两边分别乘以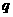 , 构造:
, 构造:
得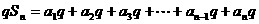 ( 3 )
( 3 )
( 2 )式两边分别对应减去( 3 )式两边,得
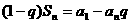
即:
综上所得: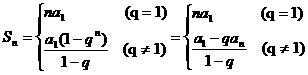
说明:①.一般资料称这种方法为错位相减法.
②.本题是题型二.
二、例题选讲
1.‘定’构造数列法与‘动’构造数列法求解数列的通项或前 项和,常
项和,常
